Có Bao Nhiêu Số Có 6 Chữ Số Khác Nhau? Lời Giải Toán Học Đầy Đủ

Trong lĩnh vực toán học tổ hợp, việc xác định số lượng các số tự nhiên thỏa mãn những điều kiện nhất định là một dạng bài tập phổ biến. Một trong những câu hỏi thường gặp là “có bao nhiêu số có 6 chữ số khác nhau?”. Bài viết này sẽ hướng dẫn bạn cách giải quyết bài toán này một cách chi tiết, áp dụng các quy tắc cơ bản trong tổ hợp để tìm ra đáp án chính xác nhất.

Phân Tích Yêu Cầu Bài Toán

Để tìm số lượng các số tự nhiên có 6 chữ số khác nhau, chúng ta cần hiểu rõ các điều kiện sau:

• Số có 6 chữ số: Nghĩa là số đó phải nằm trong khoảng từ 100.000 đến 999.999. Điều này ngụ ý chữ số đầu tiên (hàng trăm nghìn) không thể là 0.
• Các chữ số khác nhau: Tất cả 6 chữ số cấu tạo nên số đó phải là đôi một phân biệt. Chúng ta có 10 chữ số để lựa chọn: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Bài toán này có thể được giải quyết hiệu quả bằng quy tắc nhân hoặc thông qua khái niệm chỉnh hợp.

Hướng Dẫn Giải Chi Tiết Bằng Quy Tắc Nhân

Chúng ta sẽ xây dựng số có 6 chữ số a₁a₂a₃a₄a₅a₆ bằng cách chọn từng chữ số từ trái sang phải, đảm bảo các điều kiện của bài toán.

Bước 1: Chọn chữ số hàng trăm nghìn (a₁)

Chữ số hàng trăm nghìn (a₁) không được là 0 (vì nếu là 0, số đó sẽ chỉ có 5 chữ số).

• Các lựa chọn cho a₁: 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Có 9 cách chọn cho a₁.

Bước 2: Chọn chữ số hàng chục nghìn (a₂)

Sau khi đã chọn được a₁, chúng ta còn lại 9 chữ số chưa được sử dụng (bao gồm cả chữ số 0 và 8 chữ số còn lại từ 1-9). a₂ có thể là 0.

• Các lựa chọn cho a₂: Bất kỳ chữ số nào trong 10 chữ số ban đầu, trừ chữ số đã chọn cho a₁.
• Có 9 cách chọn cho a₂.

Bước 3: Chọn chữ số hàng nghìn (a₃)

Lúc này, chúng ta đã sử dụng 2 chữ số khác nhau (a₁ và a₂). Còn lại 8 chữ số chưa được sử dụng.

• Các lựa chọn cho a₃: Bất kỳ chữ số nào trong 10 chữ số ban đầu, trừ 2 chữ số đã chọn cho a₁ và a₂.
• Có 8 cách chọn cho a₃.

Bước 4: Chọn chữ số hàng trăm (a₄)

Đã sử dụng 3 chữ số khác nhau (a₁, a₂, a₃). Còn lại 7 chữ số.

• Các lựa chọn cho a₄: Bất kỳ chữ số nào trong 10 chữ số ban đầu, trừ 3 chữ số đã chọn.
• Có 7 cách chọn cho a₄.

Bước 5: Chọn chữ số hàng chục (a₅)

Đã sử dụng 4 chữ số khác nhau (a₁, a₂, a₃, a₄). Còn lại 6 chữ số.

• Các lựa chọn cho a₅: Bất kỳ chữ số nào trong 10 chữ số ban đầu, trừ 4 chữ số đã chọn.
• Có 6 cách chọn cho a₅.

Bước 6: Chọn chữ số hàng đơn vị (a₆)

Đã sử dụng 5 chữ số khác nhau (a₁, a₂, a₃, a₄, a₅). Còn lại 5 chữ số.

• Các lựa chọn cho a₆: Bất kỳ chữ số nào trong 10 chữ số ban đầu, trừ 5 chữ số đã chọn.
• Có 5 cách chọn cho a₆.

Áp Dụng Công Thức Và Tính Kết Quả

Theo quy tắc nhân, tổng số các số có 6 chữ số khác nhau là tích của số cách chọn ở mỗi bước:

Tổng số = (Số cách chọn a1) × (Số cách chọn a2) × (Số cách chọn a3) × (Số cách chọn a4) × (Số cách chọn a5) × (Số cách chọn a6)
Tổng số = 9 × 9 × 8 × 7 × 6 × 5 = 136.080

Vậy, có 136.080 số có 6 chữ số khác nhau.

Giải Bài Toán Bằng Phương Pháp Chỉnh Hợp (Cách 2)

Chỉnh hợp (hoán vị có thứ tự) là một công cụ mạnh mẽ trong tổ hợp để giải quyết các bài toán sắp xếp các phần tử từ một tập hợp lớn hơn.

Tổng số cách chọn 6 chữ số từ 10 chữ số và sắp xếp chúng theo thứ tự (tạm thời không xét đến điều kiện a₁ ≠ 0) là số chỉnh hợp chập 6 của 10, ký hiệu A⁶₁₀ hoặc P(10, 6):

A⁶₁₀ = 10! / (10-6)! = 10 × 9 × 8 × 7 × 6 × 5 = 151.200

Tuy nhiên, trong số này bao gồm các trường hợp mà chữ số hàng trăm nghìn (a₁) là 0. Chúng ta cần loại bỏ các trường hợp này.

Nếu a₁ = 0, thì 5 chữ số còn lại (a₂a₃a₄a₅a₆) phải là các chữ số khác nhau được chọn từ 9 chữ số còn lại (1, 2, …, 9). Số cách chọn và sắp xếp 5 chữ số từ 9 chữ số là chỉnh hợp chập 5 của 9, ký hiệu A⁵₉ hoặc P(9, 5):

A⁵₉ = 9! / (9-5)! = 9 × 8 × 7 × 6 × 5 = 15.120

Số các số có 6 chữ số khác nhau sẽ bằng tổng số chỉnh hợp trừ đi các trường hợp có chữ số 0 ở vị trí đầu tiên:

Tổng số = A^6_10 - A^5_9 = 151.200 - 15.120 = 136.080

Cả hai phương pháp đều cho ra cùng một kết quả.

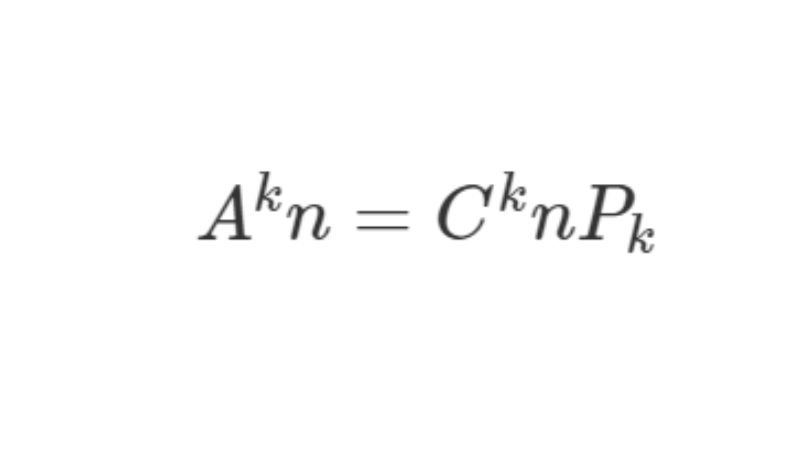
Các Dạng Bài Tập Tương Tự Và Lưu Ý

• Thay đổi số chữ số: Áp dụng tương tự cho số có 3, 4, 5… chữ số khác nhau.
• Thêm điều kiện: Ví dụ, số lẻ, số chẵn, số chia hết cho 5, hoặc có chứa/không chứa một chữ số cụ thể. Mỗi điều kiện sẽ ảnh hưởng đến số lượng lựa chọn ở các bước tương ứng.
• Lưu ý: Luôn bắt đầu từ chữ số có điều kiện ràng buộc (thường là chữ số đầu tiên không được là 0) để tránh sai sót.

Kết Luận

Qua bài viết này, chúng ta đã cùng tìm hiểu và giải chi tiết bài toán “có bao nhiêu số có 6 chữ số khác nhau” bằng hai phương pháp: quy tắc nhân và chỉnh hợp. Cả hai cách tiếp cận đều cho thấy có 136.080 số tự nhiên thỏa mãn điều kiện. Việc nắm vững các nguyên tắc này sẽ giúp bạn dễ dàng giải quyết các bài toán tổ hợp phức tạp hơn.

---

Tài liệu tham khảo:

• Sách giáo khoa Toán 11 – Đại số và Giải tích.
• Các chuyên đề về Tổ hợp và Xác suất.