Toán học lớp 6 mở ra một chương mới đầy thú vị và quan trọng với chuyên đề về tập hợp, mà trọng tâm là tập hợp các số tự nhiên lớp 6. Đây không chỉ là kiến thức nền tảng giúp các em làm quen với cách tư duy logic trong toán học mà còn là kim chỉ nam cho việc học các chương tiếp theo như số nguyên, phân số, hay số thập phân. Việc nắm vững khái niệm, các ký hiệu, và cách biểu diễn tập hợp số tự nhiên là vô cùng cần thiết, giúp học sinh xây dựng một nền tảng vững chắc để chinh phục môn Toán. Bài viết này của lvt.edu.vn sẽ cung cấp cho các em học sinh lớp 6, quý phụ huynh, và các thầy cô giáo một cái nhìn toàn diện, sâu sắc về lý thuyết và tổng hợp các dạng bài tập điển hình về tập hợp các số tự nhiên lớp 6, kèm theo lời giải chi tiết và dễ hiểu nhất.
1. Tập hợp số tự nhiên là gì? Ký hiệu tập hợp số tự nhiên
Các số tự nhiên là những số cơ bản và quen thuộc nhất mà chúng ta sử dụng hàng ngày để đếm hoặc biểu thị số lượng. Trong Toán học lớp 6, việc hiểu rõ về khái niệm tập hợp N lớp 6 và cách ký hiệu chúng là bước đầu tiên và quan trọng nhất.
Khái niệm tập hợp N lớp 6
Trong toán học, tập hợp N lớp 6 là tập hợp của tất cả các số tự nhiên. Các số tự nhiên bao gồm số 0 và các số nguyên dương (số đếm) như 1, 2, 3, 4, và cứ tiếp tục như vậy, không có điểm dừng.
Tập hợp các số tự nhiên được ký hiệu bằng chữ cái in hoa N.
Chúng ta có thể viết tập hợp N như sau:
N = {0; 1; 2; 3; 4; …}
Mỗi số tự nhiên có thể được biểu diễn bằng một điểm trên một tia số. Tia số là một đường thẳng có điểm gốc (thường là điểm 0) và có một chiều (thường là chiều từ trái sang phải) được quy định để biểu diễn các số. Mỗi số tự nhiên tương ứng với một điểm duy nhất trên tia số đó. Điểm biểu diễn số tự nhiên $a$ được gọi là điểm $a$.
- Ví dụ: Trên tia số, điểm gốc là 0. Điểm 1 cách điểm 0 một đơn vị độ dài, điểm 2 cách điểm 1 một đơn vị độ dài, và cứ thế tiếp tục.
Phân biệt tập hợp N và N*
Ngoài tập hợp N, chúng ta còn gặp một tập hợp con quan trọng khác của các số tự nhiên là tập hợp các số tự nhiên khác 0. Tập hợp này được ký hiệu là N* (đọc là N sao).
- Tập hợp N* bao gồm tất cả các số tự nhiên nhưng không bao gồm số 0.
- N* = {1; 2; 3; 4; …}
- Sự khác biệt chính:
- N chứa số 0.
- N* không chứa số 0.
- Mẹo nhớ: Chữ “sao” (*) có thể tượng trưng cho “khác 0”.
Việc phân biệt rõ ràng giữa N và N* là rất quan trọng khi giải các bài tập về tập hợp các số tự nhiên lớp 6, đặc biệt là khi bài toán yêu cầu các số tự nhiên “khác 0” hoặc “nguyên dương”.
2. Các cách viết một tập hợp các số tự nhiên
Khi làm việc với tập hợp các số tự nhiên lớp 6, chúng ta có thể biểu diễn một tập hợp bằng nhiều cách khác nhau tùy thuộc vào đặc điểm của các phần tử trong tập hợp đó. Có hai phương pháp chính để viết một tập hợp: liệt kê các phần tử hoặc chỉ ra tính chất đặc trưng của chúng.
Phương pháp liệt kê các phần tử
Đây là cách phổ biến và trực quan nhất để viết một tập hợp. Chúng ta sẽ liệt kê tất cả các phần tử của tập hợp bên trong dấu ngoặc nhọn {} và cách nhau bởi dấu chấm phẩy ;.
- Đặc điểm:
- Mỗi phần tử chỉ được liệt kê một lần.
- Thứ tự các phần tử trong tập hợp không quan trọng.
- Nếu tập hợp có nhiều phần tử mà có quy luật, hoặc là tập hợp vô hạn, chúng ta có thể dùng dấu ba chấm
...để biểu thị các phần tử còn lại theo quy luật.
- Ví dụ:
- Ví dụ 1: Tập hợp $A$ gồm các số tự nhiên nhỏ hơn 5.
- $A = {0; 1; 2; 3; 4}$
- Ví dụ 2: Tập hợp $B$ gồm các số tự nhiên chẵn nhỏ hơn 10.
- $B = {0; 2; 4; 6; 8}$ (hoặc $B = {8; 2; 0; 6; 4}$ đều đúng).
- Ví dụ 3: Tập hợp $C$ gồm các số tự nhiên lẻ.
- $C = {1; 3; 5; 7; …}$ (dùng dấu ba chấm vì tập hợp này vô hạn).
- Ví dụ 1: Tập hợp $A$ gồm các số tự nhiên nhỏ hơn 5.
Phương pháp chỉ ra tính chất đặc trưng
Khi các phần tử của một tập hợp có một hoặc nhiều tính chất chung mà chỉ những phần tử đó mới có, chúng ta có thể sử dụng phương pháp này. Phương pháp này thường được dùng cho các tập hợp có nhiều phần tử hoặc tập hợp vô hạn mà khó liệt kê hết.
- Cấu trúc chung:
- Tập hợp $P = {x | x text{ có tính chất } Q}$
- Đọc là: “$P$ là tập hợp các phần tử $x$ sao cho $x$ có tính chất $Q$”.
- Ví dụ:
- Ví dụ 1: Tập hợp $A$ gồm các số tự nhiên nhỏ hơn 5.
- $A = {x in N | x < 5}$ (Đọc là: $A$ là tập hợp các số tự nhiên $x$ sao cho $x$ nhỏ hơn 5).
- Ví dụ 2: Tập hợp $B$ gồm các số tự nhiên chẵn từ 0 đến 100.
- $B = {x in N | x text{ là số chẵn và } x le 100}$
- Ví dụ 3: Tập hợp $C$ gồm các số tự nhiên lớn hơn 10.
- $C = {x in N | x > 10}$
- Ví dụ 1: Tập hợp $A$ gồm các số tự nhiên nhỏ hơn 5.
Cả hai cách viết này đều hợp lệ và được sử dụng linh hoạt trong các bài tập. Việc chọn cách viết nào phụ thuộc vào yêu cầu của bài toán và sự thuận tiện trong việc biểu diễn tập hợp.
3. Lý thuyết về tập hợp số tự nhiên lớp 6 cần nhớ
Để học tốt Toán lớp 6 tập hợp số tự nhiên, ngoài khái niệm và cách viết, các em cần nắm vững những tính chất cơ bản về thứ tự và các đặc điểm khác của tập hợp số tự nhiên. Đây là những lý thuyết về tập hợp số tự nhiên lớp 6 quan trọng giúp giải quyết các bài toán so sánh, tìm số liền trước, liền sau, và hiểu rõ cấu trúc của tập hợp này.
Thứ tự trong tập hợp số tự nhiên
Trong tập hợp các số tự nhiên, luôn có một sự sắp xếp theo thứ tự.
- So sánh hai số tự nhiên: Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia.
- Khi số $a$ nhỏ hơn số $b$, ta viết $a < b$ (đọc là $a$ nhỏ hơn $b$).
- Hoặc ta có thể viết $b > a$ (đọc là $b$ lớn hơn $a$).
- Ví dụ: $3 < 5$ hoặc $5 > 3$.
- Ký hiệu “nhỏ hơn hoặc bằng” và “lớn hơn hoặc bằng”:
- Ta viết $a le b$ để chỉ rằng $a$ nhỏ hơn $b$ hoặc $a$ bằng $b$.
- Ta viết $b ge a$ để chỉ rằng $b$ lớn hơn $a$ hoặc $b$ bằng $a$.
- Ví dụ: $a$ là số tuổi của bạn, $b$ là số tuổi của anh bạn. Nếu bạn nhỏ tuổi hơn hoặc bằng tuổi anh bạn, ta viết $a le b$.
- Biểu diễn trên tia số:
- Trên tia số, điểm biểu diễn số nhỏ hơn luôn nằm ở bên trái điểm biểu diễn số lớn hơn.
- Ví dụ: Điểm 3 nằm bên trái điểm 5 trên tia số.
- Tính chất bắc cầu: Nếu $a < b$ và $b < c$ thì chắc chắn $a < c$.
- Ví dụ: Nếu bạn A cao hơn bạn B, và bạn B cao hơn bạn C, thì chắc chắn bạn A cao hơn bạn C.
Các tính chất quan trọng
Tập hợp số tự nhiên có những đặc điểm riêng biệt và quan trọng mà các em cần ghi nhớ:
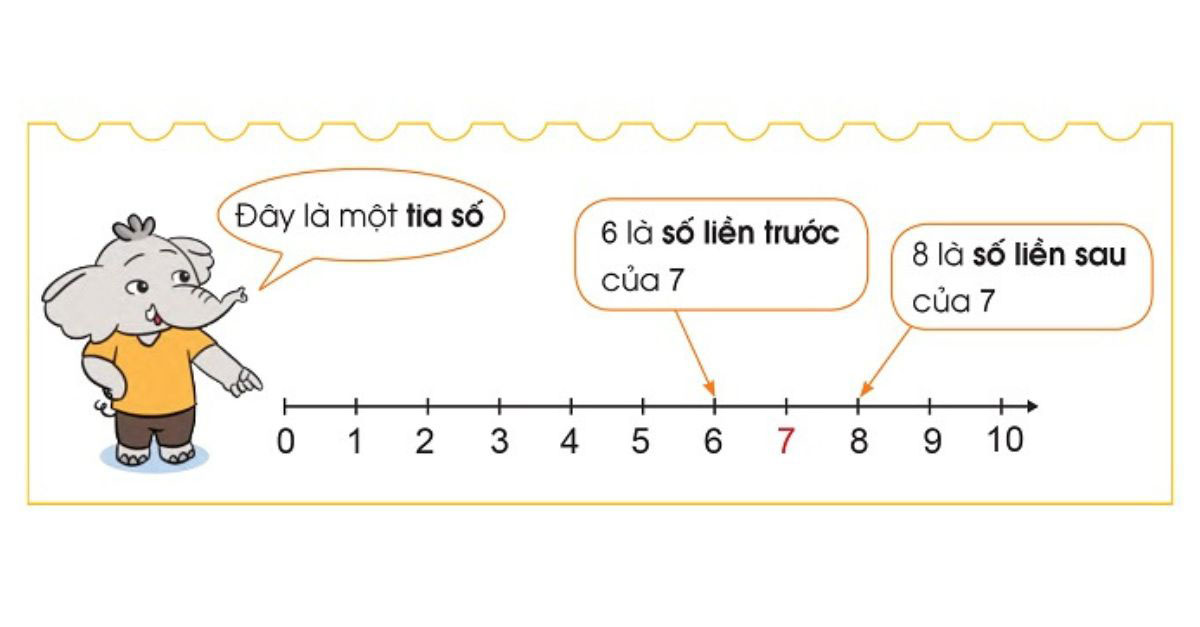
- Số liền sau và số liền trước:
- Mỗi số tự nhiên (trừ số 0) đều có một số liền trước và một số liền sau.
- Mỗi số tự nhiên đều có một số liền sau duy nhất. Số liền sau của một số tự nhiên $a$ là $a+1$.
- Ví dụ:
- Số 1 là số liền sau của số 0.
- Số 6 là số liền sau của số 5.
- Khi đó, ta cũng nói số 0 là số liền trước của số 1, số 5 là số liền trước của số 6.
- Lưu ý: Số 0 không có số tự nhiên liền trước.
- Số tự nhiên nhỏ nhất:
- Số 0 là số tự nhiên nhỏ nhất. Điều này có nghĩa là không có số tự nhiên nào nhỏ hơn 0.
- Không có số tự nhiên lớn nhất:
- Tập hợp các số tự nhiên không có số lớn nhất. Dù bạn chọn số tự nhiên nào lớn đến đâu, bạn vẫn có thể tìm thấy một số tự nhiên khác lớn hơn nó (ví dụ, bằng cách cộng thêm 1). Điều này cho thấy tập hợp số tự nhiên là một tập hợp vô hạn.
- Số phần tử của tập hợp N:
- Tập hợp số tự nhiên có vô số phần tử.
Việc hiểu rõ các tính chất của tập hợp N toán lớp 6 sẽ giúp các em tự tin hơn khi giải các bài toán liên quan đến so sánh, sắp xếp thứ tự, và xác định các phần tử trong một tập hợp cụ thể. Đây là nền tảng vững chắc để tiếp tục học các kiến thức toán học phức tạp hơn.
4. Tổng hợp các dạng bài tập tập hợp số tự nhiên lớp 6 (có lời giải)
Để củng cố chuyên đề về tập hợp N toán 6, việc thực hành qua các dạng bài tập là không thể thiếu. Dưới đây là tổng hợp các dạng bài tập tập hợp số tự nhiên lớp 6 thường gặp nhất, kèm theo ví dụ minh họa và lời giải chi tiết, giúp các em ôn tập và nắm vững kiến thức.
Dạng 1: Viết tập hợp theo yêu cầu
Đây là dạng bài tập cơ bản nhằm kiểm tra khả năng biểu diễn tập hợp bằng hai cách: liệt kê các phần tử và chỉ ra tính chất đặc trưng.
- Phương pháp giải:
- Đọc kỹ yêu cầu đề bài để xác định các phần tử của tập hợp.
- Nếu tập hợp có ít phần tử, hoặc có quy luật rõ ràng, dễ viết, nên dùng cách liệt kê.
- Nếu tập hợp có quá nhiều phần tử hoặc là vô hạn và có tính chất chung, nên dùng cách chỉ ra tính chất đặc trưng.
- Bài tập ví dụ:
- Bài 1: Viết tập hợp $A$ các số tự nhiên lớn hơn 5 và nhỏ hơn 12 bằng cách liệt kê các phần tử.
- Bài 2: Viết tập hợp $B$ các số tự nhiên lẻ lớn hơn 10 bằng cách chỉ ra tính chất đặc trưng.
- Bài 3: Viết tập hợp $C$ các số tự nhiên chẵn nhỏ hơn hoặc bằng 20 bằng cả hai cách.
- Lời giải:
- Bài 1: Các số tự nhiên lớn hơn 5 và nhỏ hơn 12 là 6, 7, 8, 9, 10, 11.
- Vậy $A = {6; 7; 8; 9; 10; 11}$.
- Bài 2: Các số tự nhiên lẻ lớn hơn 10 là 11, 13, 15, …
- Vậy $B = {x in N | x text{ là số lẻ và } x > 10}$.
- Bài 3: Các số tự nhiên chẵn nhỏ hơn hoặc bằng 20 là 0, 2, 4, …, 20.
- Cách liệt kê: $C = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18; 20}$.
- Cách chỉ ra tính chất đặc trưng: $C = {x in N | x text{ là số chẵn và } x le 20}$.
- Bài 1: Các số tự nhiên lớn hơn 5 và nhỏ hơn 12 là 6, 7, 8, 9, 10, 11.
Dạng 2: Xác định số phần tử của tập hợp
Dạng bài này yêu cầu đếm số lượng phần tử trong một tập hợp.
- Phương pháp giải:
- Nếu tập hợp được liệt kê, chỉ cần đếm số phần tử.
- Nếu tập hợp được cho dưới dạng tính chất đặc trưng và các phần tử tạo thành một dãy số cách đều (cấp số cộng), ta dùng công thức:
Số phần tử = (Số cuối – Số đầu) / Khoảng cách + 1
- Bài tập ví dụ:
- Bài 1: Cho tập hợp $M = {2; 4; 6; 8; 10}$. Hỏi tập hợp $M$ có bao nhiêu phần tử?
- Bài 2: Tập hợp $P$ gồm các số tự nhiên từ 1 đến 100. Hỏi $P$ có bao nhiêu phần tử?
- Bài 3: Tập hợp $Q$ gồm các số tự nhiên có hai chữ số và chia hết cho 5. Hỏi $Q$ có bao nhiêu phần tử?
- Lời giải:
- Bài 1: Đếm trực tiếp các phần tử: 2, 4, 6, 8, 10. Có 5 phần tử.
- Vậy tập hợp $M$ có 5 phần tử.
- Bài 2: Các số tự nhiên từ 1 đến 100 là 1, 2, 3, …, 100.
- Số phần tử = (100 – 1) / 1 + 1 = 99 + 1 = 100.
- Vậy tập hợp $P$ có 100 phần tử.
- Bài 3: Các số tự nhiên có hai chữ số và chia hết cho 5 là 10, 15, 20, …, 95.
- Đây là một dãy số cách đều 5 đơn vị. Số đầu là 10, số cuối là 95.
- Số phần tử = (95 – 10) / 5 + 1 = 85 / 5 + 1 = 17 + 1 = 18.
- Vậy tập hợp $Q$ có 18 phần tử.
- Bài 1: Đếm trực tiếp các phần tử: 2, 4, 6, 8, 10. Có 5 phần tử.
Dạng 3: Sử dụng ký hiệu ∈ và ∉
Dạng này kiểm tra khả năng nhận biết một phần tử có thuộc tập hợp hay không.
- Phương pháp giải:
- Sử dụng ký hiệu “∈” (thuộc) nếu phần tử nằm trong tập hợp.
- Sử dụng ký hiệu “∉” (không thuộc) nếu phần tử không nằm trong tập hợp.
- Bài tập ví dụ:
- Điền ký hiệu thích hợp (∈ hoặc ∉) vào chỗ trống:
- a) 15 … N
- b) 0 … N*
- c) -3 … N
- d) 20 … Tập hợp các số tự nhiên nhỏ hơn 20
- Điền ký hiệu thích hợp (∈ hoặc ∉) vào chỗ trống:
- Lời giải:
- a) 15 ∈ N (Vì 15 là số tự nhiên).
- b) 0 ∉ N* (Vì N* là tập hợp các số tự nhiên khác 0).
- c) -3 ∉ N (Vì -3 là số nguyên âm, không phải số tự nhiên).
- d) 20 ∉ Tập hợp các số tự nhiên nhỏ hơn 20 (Vì 20 không nhỏ hơn 20).
Dạng 4: Bài tập nâng cao
Dạng này thường yêu cầu kết hợp nhiều kiến thức hoặc có điều kiện phức tạp hơn.
- Phương pháp giải:
- Phân tích kỹ các điều kiện của bài toán.
- Kết hợp các quy tắc về thứ tự, số liền trước/sau, tính chất chia hết (nếu có).
- Viết tập hợp và kiểm tra lại.
- Bài tập ví dụ:
- Bài 1: Cho $A = {x in N | 10 < x le 25 text{ và } x text{ là số lẻ}}$.
- a) Viết tập hợp $A$ bằng cách liệt kê các phần tử.
- b) Tính tổng các phần tử của $A$.
- Bài 2: Tìm số tự nhiên $k$ lớn nhất sao cho $k$ là số liền sau của một số tự nhiên có ba chữ số.
- Bài 1: Cho $A = {x in N | 10 < x le 25 text{ và } x text{ là số lẻ}}$.
- Lời giải:
- Bài 1:
- a) Các số tự nhiên $x$ thỏa mãn $10 < x le 25$ là 11, 12, …, 25.
- Trong đó, các số lẻ là: 11, 13, 15, 17, 19, 21, 23, 25.
- Vậy $A = {11; 13; 15; 17; 19; 21; 23; 25}$.
- b) Tổng các phần tử của $A$: $11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 = 144$.
- a) Các số tự nhiên $x$ thỏa mãn $10 < x le 25$ là 11, 12, …, 25.
- Bài 2:
- Số tự nhiên có ba chữ số nhỏ nhất là 100, lớn nhất là 999.
- Số liền sau của một số tự nhiên $a$ là $a+1$.
- Để $k$ lớn nhất, thì số tự nhiên mà $k$ là số liền sau của nó phải là số tự nhiên có ba chữ số lớn nhất, tức là 999.
- Vậy $k = 999 + 1 = 1000$.
- $k$ là số liền sau của số 999.
- Bài 1:
Việc luyện tập thường xuyên các dạng bài tập tập hợp số tự nhiên lớp 6 này sẽ giúp các em tự tin hơn và nắm chắc kiến thức để áp dụng vào các bài kiểm tra và các chuyên đề toán học nâng cao hơn.
Kết thúc chương tập hợp các số tự nhiên lớp 6 là việc các em đã trang bị cho mình những khái niệm cơ bản nhất về số học và tư duy tập hợp. Chúng ta đã cùng nhau tìm hiểu về định nghĩa của tập hợp N và N*, các cách viết một tập hợp, và những tính chất quan trọng về thứ tự trong tập hợp số tự nhiên. Đồng thời, việc giải các dạng bài tập từ cơ bản đến nâng cao đã giúp củng cố lý thuyết và rèn luyện kỹ năng vận dụng.
Nắm vững chương này không chỉ là điểm cộng trong các bài kiểm tra Toán lớp 6 mà còn là nền tảng vững chắc cho hành trình khám phá thế giới số học rộng lớn hơn. Hãy tiếp tục luyện tập và khám phá để biến kiến thức thành kỹ năng, phục vụ tốt cho con đường học tập của mình!
Tài liệu tham khảo:
- Sách giáo khoa Toán 6 – Bộ Kết nối tri thức với cuộc sống.
- Sách giáo khoa Toán 6 – Bộ Chân trời sáng tạo.
- Sách giáo khoa Toán 6 – Bộ Cánh diều.
